| Этот урок касается такой важной темы, как коллизии. В прошлой статье на http://gamer-club.ucoz.com товарищ DarkMedveD рассказывал о коллизии изображений на плоскости, я же расскажу о пересечениях в пространстве. Сначала о точках =) Самое простое, конечно, это пересечение со сферой, можно просто из формулы расстояния между векторами вычислить расстояние от центра сферы до нашей точки и сравнить это с её радиусом. Но формула длины вектора предполагает вычисление корня, что тормозило бы прогу(чуток)), поэтому можно от этого избавиться, возведя обе стороны ур-ия в квадрат. Итак, имеем:
Code
function PointInSphere(A,O: TVector; r: single): boolean;
begin
Result:=VectorSqrDistance(A,O)<=Sqr(r);
end;
Что каксается коробки, то тут всё сложнее. Предположим, что точка находится в объёме коробки. Тогда можно заметить, что проекции на все 3 оси коробки, ориентированной произвольно, будут меньше соответствующих размеров коробки. 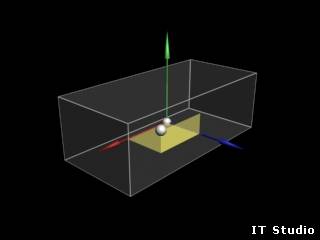
При выходе за пределы объёма проекции соответственно будут больше и не попадут туда. Как я уже сказал, это справедливо для ориентированной в любом направлении коробки. А проекцией вектора на вектор, как вам, вероятно, известно, является их скалярное произведение, умноженное на длину проецируемого вектора. Пусть А - точка, О - центр коробки, D - вектор оси Х коробки, U - вектор оси Y коробки, L - вектор оси Z коробки. Имеем код: Code
function PointInBox(A,O,D,U,L: TVector): boolean;
var szl,szw,szh: single;
begin
A:=VectorSubtract(A,O);
szl:=VectorSqrLength(D);
szw:=VectorSqrLength(L);
szh:=VectorSqrLength(U);
O.x:=Sqr(VectorDotProduct(A,D))/szl;
O.y:=Sqr(VectorDotProduct(A,U))/szh;
O.z:=Sqr(VectorDotProduct(A,L))/szw;
Result:=(O.x <= szl)and(O.y <= szh)and(O.z <= szw);
end;
Это были основные стереометрические объёмы, применяющиеся в CG, но в заключение приведу пример проверки вхождения точки в объём эллипсоида вращения (тело, полученное при вращении эллипса вокруг одной из его осей). Решать проблему "в лоб" нерационально, поэтому легче привести данные задачи к условиям сферы =)
Здесь пара доп. функций:
VectorInverse: V[i] = 1/V[i]
VectorCombine: V1[i] = V1[i]*V2[i]
Вектор Scale - размеры эллипсоида по 3-м его осям.
Примечание: данный код справедлив только для эллипсоида, ориентированного по матрице
|1 0 0|
|0 1 0|
|0 0 1|
, для ориентированного по-другому можно просто домножить вектор к нашей точке на соответствующую матрицу. Code
function PointInEllipsoid(A,O,Scale: TVector): boolean;
begin
Scale:=VectorInverse(Scale);
A:=VectorSubtract(A,O);
O:=Vector0;
A:=VectorCombine(A,Scale);
Result:=PointInSphere(A,O,1);
end;
Вот, пожалуй, и всё на сегодня, успехов в CG =)
| 
